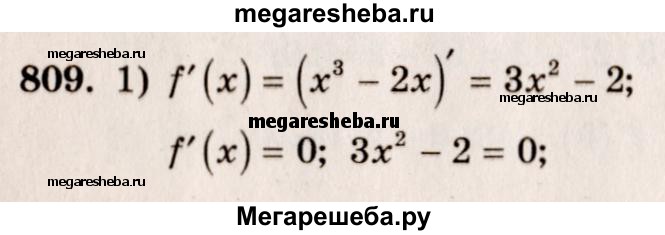ГДЗ по алгебре 10‐11 класс Алимов Базовый и углубленный уровень упражнение - 809

Авторы: Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.
Тип: Учебник, Базовый и углубленный уровень
Подробный решебник (ГДЗ) по Алгебре за 10‐11 (десятый‐одиннадцатый) класс - готовый ответ упражнение - 809. Авторы учебника: Алимов, Колягин, Ткачева, Базовый и углубленный уровень 2015-2024.
809. Найти значения х, при которых значение производной функции f (х) равно 0, если: 1) f (х) = х^3 — 2х; 2) f (х) = -х^2 + Зх + 1; 3) f (х) = 2х^3 + Зх^2 - 12х - 3; 4) f (х) = х^3 + 2х^2 - 7х + 1; 5) f (х) = Зх^4 - 4х^3 - 12х^2; 6) f (х) = х^4 + 4х^3 - 8х^2 - 5.